
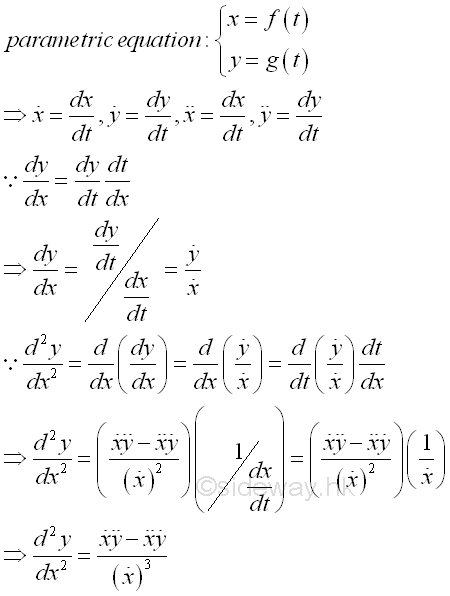
Notice on our graph that the curve intersects itself! Don’t worry, I will not ask you to find where this is (nor will the BC exam)…however you will be asked the following: A curve defined by x(t) =… and y(t) = … intersects itself at the point (5,0). Divide by dx/dt.ĩ For the graph of the parametric curve described above, find the interval(s) where the curve is concave down.ġ0 How can we use to find the locations of anyġ1 Gee…it sure would be nice if we could use our GC to find some of this information we just did by hand!!! Let’s use our GC to check our answers to some of the problems we completed… We will try both in graphing mode and from the home screen!ġ2 Notice on our graph that the curve intersects itself Find the derivative of dy/dx with respect to t. To find the second derivative of a parametrized curve, we find the derivative of the first derivative: 1. Does this match with our graph?ħ What do we need to find the intervals on which the tangent lines are decreasing? I.O.W….where the graph of the curve is _.
Equation of tangent line? Does this match with our graph? c.) Find the equation of the tangent line at t=3 d.) Find the intervals of t during which the tangent lines have positive slope. Equation of tangent line? Does this match with our graph? GRAPH IN YOUR GC TO SEE!!!, b.) Find the value(s) of t at which the curve described above has a vertical tangent line. c.) Find each of the following and discuss their meaningĥ Finding Vertical and Horizontal TangentsĦ a.) Find the value(s) of t at which the curve described above has a horizontal tangent line. How would one go about differentiating a pair of parametric equations?.It is not too bad…but check out how we get to a process that is “not too bad.”Ĥ a.) Graph the above on the interval by hand.ī.) Find the equation of the line tangent to the curve at t= 4. – SAME CONCEPTS…DIFFERENT FUNCTIONSĢ How would one go about differentiating a pair of parametric equations So we will find derivatives and integrals and interpret their meanings. Parametric curves have tangent lines, rates of change, area under and above, local and absolute maxima and minima, horizontal and vertical tangents, etc.


 0 kommentar(er)
0 kommentar(er)
